مقدمه

با توجه به گستردگی و همچنین پایین بودن ولتاژ در شبکه های توزیع، تلفات انرژی در این شبکه ها قابل توجه است. یک از روشهای کاهش تلفات این شبکه ها، تغییر آرایش آنها برای بارهای مختلف می باشد. از طرفی با توجه به تمایل روزافزون به خودکار سازی (اتوماسیون) شبکه های توزیع، امکان کنترل و تغییر آرایش این شبکه ها روز به روز سهل تر می شود. تجدید آرایش (بازآرائی) شبكه ممكن است به منظورهای متفاوتی انجام شود. در شرایط بهره برداری عادی از شبكه، تجدید آرایش آن به منظور كاهش تلفات شبکه [ 1,2 ] و ایجاد توازن بارگذاری روی فیدرها انجام می گیرد[ 3]. در شرایطی كه خطای دائم ایجاد شده است، تجدید آرایش شبكه برای برگرداندن سرویس دهی مشتركان و به حداقل رساندن نواحی بدون برق بكار می رود[ 4]. در این مقاله تجدید آرایش برای داشتن كمترین تلفات مدنظر است.

تاكنون روشهای متعددی برای حل مساله تجدید آرایش شبكه های توزیع ارائه شده است. یك دسته از این روشها، با "جستجوهای ابتكاری" آرایش بهینه را پیدا می كنند [ 1,2 ] . برخی دیگر از روشها با استفاده از هوش مصنوعی [ 5]، الگوریتم ژنتیک [ 6,8 ] و شبیه سازی ذوب فلزات [ 7] آرایش بهینه را معرفی می كنند. در این بخش الگوریتم دایسترا برای یافتن آرایش بهینه پیشنهاد شده است و نحوه کاربرد آن برای دو شبکه توزیع نمونه ارائه شده است و نشان داده شده است که این روش اولا آرایش بهینه مطلق را در اختیار می گذارد.

ثانیا با توجه به نکاتی که در بکار بستن آن پیشنهاد شده است، حجم محاسبات این روش بسیار کم بوده و از سرعت محاسباتی بالائی برخوردار است بطوریکه برای استفاده در زمان واقعی مناسب می باشد.

در ادامه ابتدا الگوریتم دایسترا معرفی می شود. سپس نحوه کاربرد این الگوریتم برای حل مساله تجدید آرایش بیان می شود. آنگاه نتایج کاربرد آن برای دو شبکه نمونه یک حلقه ای و پنج حلقه ای ارائه می گردد.

سپس روش پیشنهادی با سایر روشها مقایسه شده ودر نهایت نتایج این بخش بیان می شود.

 

-2 الگوریتم دایسترا

الگوریتم دایسترا در نظریه گراف اصولا برای حل مساله کوتاهترین مسیر بکارمی رود [ 9]. یک نمونه از یک شبکه راه آهن تعدادی شهرهای مختلف را به یکدیگر » : مساله کوتاهترین مسیر به این صورت بیان می شود این مساله در «. متصل می کند. هدف پیداکردن کوتاهترین راه بین دو شهر مشخص از این شبکه می باشد حقیقت یک مساله بهینه سازی است که به یافتن یک زیرگراف خاص با کمترین وزن در یک گراف وزندار منتهی می شود. در این مساله نمونه، وزنها نماینده فاصله ریلی بین هر دو شهر می باشند که مستقیما به یکدیگر متصل اند. به کمک مثال زیر، الگوریتم دایسترا برای حل مساله کوتاهترینفاصله را توضیح می دهیم.

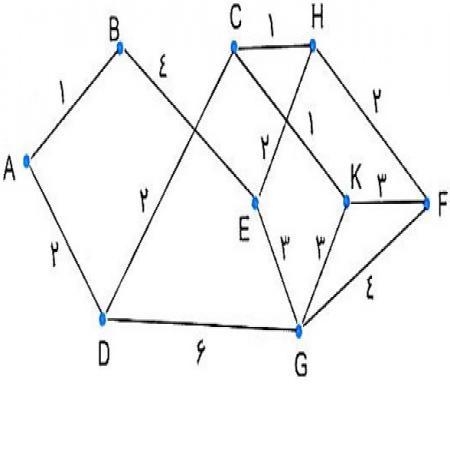
مثال: گراف شکل 1- الف را در نظر می گیریم. در این گراف وزن هر یال بر روی آن یال نوشته شده است. می خواهیم زیرگرافی را پیدا کنیم که کوتاهترین فاصله بین گرهu0 با سایر گره ها را مشخص کند. این زیرگراف را زیرگراف بهینه می نامیم. برای این منظور به ترتیب زیر عمل می کنیم.

u دارد، مرحله اول: تمام یالهای متصل به گره شروعu0 را بررسی نموده و از میان آنها، یالی که کمترین وزن را مشخص می کنیم.

این یال اولین یال زیرگراف بهینه خواهد بود. در گراف شکل 1- الف یالهائی که وزن متصل اند و یال با وزن 1 کمترین وزن را دارد. بنابراین زیرگراف بهینه در مرحله اول u 7 و 2 دارند به گره 0 ،1 شامل یال با وزن 1 می باشد که در شکل 1-ب نشان داده شده است.

مرحله دوم: از میان یالهای باقیمانده گراف اولیه، همه یالهائی که فقط از یک طرف به زیرگراف بهینه مرحله قبل وصل هستند، را درنظر می گیریم. که در اینجا یالهائی با وزن 7و 2 و 3 و 4 هستند .هر یك از این یالها را به ترتیب به زیرگراف بهینه مرحله قبل می افزائیم که در نتیجه. به ازای هر یک از این یالها، طول مسیری از زیر گراف حاصل آن را بدست می آوریم كه گره u0 را به گره جدید اضافه شده وصل می کند، آن یالی ، کوتاهترین مسیر را دارد؛ عنصر دوم زیرگراف بهینه خواهد بود. برای گراف این مثال بترتیب یالهای 7 و 2 و 3 و 4 ، مسیرهایی بطول 7و 2 و 1 3 و 1 4 ایجاد می کنند که یال 2 کمترین مسیر را دارد. پس زیرگراف بهینه مرحله دوم شامل یالهای با وزن ‌‌{1,2} می باشد که در شکل 1-ج نشان داده شده است.

مرحله سوم: مرحله سوم را مانند مرحله دوم برای باقیمانده گراف عینا تکرار می کنیم. همه یالهائی که فقط، از یک طرف به زیرگراف بهینه مرحله قبل وصل هستند عبارتند از: 7 و 3 و 4 و 5 و 8 همچنین طول مسیرهای بین گره u0 تا گره های جدید ایجاد شده عبارت است از : 7 و 1 3 و 1 4 و 2 5 و 2 8 که کوچکترین آنها 1 3 می باشد که یال متناظر با آن، یال با وزن 3 می باشد و باید به زیرگراف بهینه اضافه شود. پس زیرگراف بهینه این، مرحله شامل یالهای با وزن {3,2,1} می باشد كه در شكل 1- د نشان داده شده است .

مرحله چهارم: مرحله چهارم را مانند مرحله سوم برای باقیمانده گراف اصلی عینا تکرار می کنیم. همه، یالهائی که فقط از یک طرف به زیرگراف بهینه مرحله قبل وصل هستند عبارتند از :4 و 6 و 8.

. همچنین طول مسیر ها بین گره u0 تا گره های جدید ایجاد شده عبارتند از : 1 4 و 1 3 6 و 2 8 كه كوچكترین آنها 1 4 می باشد که یال متناظر با آن، یال با وزن 4 می باشد و باید به زیرگراف بهینه اضافه شود. پس زیرگراف بهینه این مرحله شامل یالها با وزن {4,3,2,1} می باشد كه در شكل الف - ه نشان داده شده است .

. اکنون چون زیرگراف بهینه حاصل همه گرههای گراف اصلی را در برگرفته است، مراحل الگوریتم دایسترا پایان یافته است و كمترین فاصله گره u0 تا سایر گره ها، مسیرهای روی زیرگراف بهینه حاصل یعنی زیر گراف شکل 1 – ه می باشند .

-3 روش جدید پیشنهادی برای تجدید آرایش شبكه توزیع

یک شبکه توزیع از تعدادی فیدر تشکیل شده است که از یک یا چند پست فوق توزیع تغذیه می شوند. خطوطی وجود دارند که فیدرها را می توانند به یکدیگر متصل کنند و تشکیل یک حلقه دهند. اصولا شبکه های توزیع با حلقه های کم طراحی می شوند ولی به صورت شعاعی بهره برداری می شوند . یعنی حلقه ها در هنگام بهره برداری بصورت باز می باشند . بنابراین برای شبکه توزیع آرایشهای متفاوت وجود دارد که با توجه به بارهای شبکه می توان آرایشی را بکار برد که کمترین تلفات را داشته باشد. این آرایش را آرایش بهینه می نامیم. یكی از مشكلات یافتن آرایش بهینه این است كه تعداد آرایشها بسیار زیاد است و عملا نمی توان با بررسی همه آنها آرایش بهینه را بدست آورد . بنابراین به الگوریتمهای ابتکاری و یا الگوریتمهایی مانند الگوریتم ژنتیک و یا شبیه سازی ذوب فلزات متوسل می شوند . در این مقاله، الگوریتم دایسترا برای یافتن آرایشی که کمترین تلفات را دارد؛ پیشنهاد شده است که در زیر توضیح داده می شود.

در صورتیکه تمام خطوط یک شبکه توزیع بسته باشند، یک شبکه توزیع بسته بدست می آید که گراف آنرا بعنوان گرا ف اولیه در نظر می گیریم . گره شروع گراف را گره مبنا (باس بی نهایت) که همان گره پستهای فوق توزیع می باشد، در نظر می گیریم . در الگوریتم دایسترا کمترین فاصله مورد نظر بود ولی در اینجا به دنبال کمترین تلفات می باشیم . تلفات خطوط به مقاومت اهمی و جریان عبوری از خ طوط بستگی دارد. در اینجا ما بر طبق الگوریتم دایسترا از گره مبنا شروع کرده و مرحله به مرحله پیش می رویم . در هر مرحله یک خط اضافه می کنیم بطوریکه تلفات کل مسیرها کمترین مقدار باشد . مثلا در مرحله اول تمام خطوط متصل به گره مبنا را بررسی کرده و تلفات شبکه ای که از اضافه کردن هریک از آنها به گره مبنا ایجاد می شود را بوسیله پخش بار بدست می آوریم . آن خطی که کمترین تلفات را ایجاد می کند، مشخص نموده و به گره مبنا می افزائیم تا شبکه بهینه در مرحله اول بدست آید . در مرحله دوم تمام خطوطی که از یک طرف به شبکه بهینه مرحله قبل وصل می شوند را در نظر گرفته و هر دفعه یکی از خطوط مزبور را به آن شبکه وصل می کنیم و برای شبکه حاصل با انجام پخش بار تلفات را بدست می آوریم . مجددا از میان شبکه های حاصل آن شبکه ای که کمترین تلفات را ایجاد می کند، بعنوان شبکه بهینه مرحله دوم معرفی می کنی م. مراحل دیگر را مانند مرحله دوم تکرار می کنیم تا به جائی برسیم که شبکه بهینه حاصل همه گره های شبکه بسته اولیه را شامل شود.

با کمی دقت در بکار بستن الگوریتم دایسترا، ملاحظه می گردد که هر دفعه که تلفات اضافه شدن یک خط به شبکه بهینه مرحله قبل محاسبه می شود ؛ خط اضافه شده فقط در یکی از فیدرها است و فقط ساختار یکی از فیدرها تغییر می کند . از طرفی چون خطوط اضافه شده فقط از یک طرف به شبکه بهینه مرحله قبل وصل می شوند؛ هر فیدر همواره شعاعی خواهد بود . بنابراین در هر بار محاسبه تلفات فقط بایستی پخش بار شعاعی و آن هم فقط بر روی یکی از فیدرها انجام دهیم . لذا در این مقاله پخش بار شعاعی پیشرو -پسرو پیشنهاد شده است که مخصوص شبکه های شعاعی بوده و از سرعت بسیار بالائی برخوردار می باشد.

نکته دیگر این است در هر مرحله خطوط زیادی مورد بررسی قرار می گیرند یعنی هر کدام از این خطوط به یک فیدر اضافه می شوند و تلفات آنها با انجام پخش بار محاسبه می شوند ولی از میان این خطوط، فقط آن خطی که کمترین تلفات را ایجاد می کند، انتخاب می شود . سپس در مرحله بعد بسیاری از همان خطوط بررسی شده مرحله قبل، جزء خطوط مورد بررسی قرار می گیرند و معمولا در مرحل ه جدید هم باید به همان فیدر قبلی شان وصل شوند و بازهم عموما ساختار آن فیدر نسبت به مرحله قبل تغییر نمی کند . بنابراین برای این موارد دیگر نیاز به پخش بار جدید نیست و می توان در مرحله جدید از همان مقدار تلفات محاسبه شده برای آن فیدر در مرحله قبل، استفاده کرد . بدین ترتیب حجم محاسبات بسیار کاهش می یابد . لذا در هر مرحله تلفات کلیه فیدرها را برای استفاده احتمالی مرحله بعد ذخیره می کنیم .

در دو بخش بعدی نتایج اجرای روش پیشنهادی برای دو شبکه توزیع نمونه ارائه می گردد و نشان داده خواهد شد كه اولا آرایش بدست آمده توسط روش پیشنهادی، بهینه مطلق می باشد. ثانیا سرعت رسیدن به آرایش بهینه بسیار بالا می باشد.

-4 مطالعه روش پیشنهادی برای یك شبكه توزیع تك حلقه ای

در این قسمت برای مطالعة روش پیشنهادی، شبكه تك حلقه ای شكل ( 2) را در نظر می گیریم. این شبكه از 7 باس و 7 خط تشكیل شده است. اطلاعات خطوط و بارهای این شبكه در جدول ( 1) آمده است.

الگوریتم دایسترا برای شبکه تک حلقه ای فوق در 6 مرحله انجام شده است که نتایج آن در جدول 2خلاصه گردیده است. در ستون اول جدول ( 2) شماره مرحله آمده است. خطوطی که در هر مرحله از یک انتهای شان به شبکه بهینه مرحله قبل متصل اند، در ستون دوم جدول ( 2) آورده شده اند. همچنین تلفات شبکه ای که از اضافه کردن هر یک از خطوط مزبور به شبکه بهینه مرحله قبل بوجود می آید نیز در ستون دوم جدول نوشته شده است. با توجه به کمترین تلفات، شبکه بهینه حاصل هر مرحله در ستون سوم جدول ( 2) بیان گردیده است.

ملاحظه می شود که پس از 6 مرحله شبکه بهینه حاصل شامل خطوط 1-7-2-6-3-5 می باشد ( خط 4 را شامل نمی شود ) یعنی خط 4 باید باز باشد.

چنانکه در ستون دوم جدول ( 2) ملاحظه می شود، در بسیاری از موارد یک خط در دو مرحله متوالی جزء خطهای مورد بررسی می باشد و در هر دو مرحله به یک فیدر یکسان اضافه می شود که عمدتا ساختار این فیدر در دو مرحله تغییر نمی کند. بنابراین در این موارد در مرحله جدید پخش بار انجام نداده ایم و از تلفات محاسبه شده برای آن فیدر در مرحله قبل استفاده کرده ایم. در شبکه فوق کلا 7 دفعه پخش بار روی فیدرهای شعاعی انجام گرفته است و فیدرهائی که برروی آنها پخش بار انجام شده است؛ بطور متوسط تعداد 2.2857 خط داشته اند. بنابراین محاسبات مورد نیاز بسیار کم می باشد. کل زمان محاسبه برای بدست آوردن آرایش بهینه شبکه یک در MATLAB حلقه ای فوق 0.157 ثانیه بوده است. این محاسبه توسط یک برنامه کامپیوتری با نرم افزار یک کامپیوتر پنتیوم 2.4 گیگاهرتز صورت گرفته است.

برای شبکه یک حلقه ای فوق چون فقط یک خط باید باز باشد می توان تمام حالتهای قطع یک خط را مورد بررسی قرار داده و تلفات آن را با استفاده از پخش بار بدست آورد و حالت کمترین تلفات را تعیین نمود. این کار انجام شده است و نتایج در جدول ( 3) خلاصه شده است ملاحظه می شود که حالت کمترین تلفات در هنگام قطع خط 4 است که از روش الگوریتم دایسترا نیز به همین حالت بهینه رسیدیم.

-5 مطالعة روش پیشنهادی برای یك شبكه توزیع پنج حلقه ای

برای بررسی مساله تجدید آرایش شبكه توزیع به روش پیشنهادی، یك شبكه توزیع را كه معمولا برای همین منظور بكار برده شده [ 1,2,11 ] انتخاب نموده ایم. اطلاعات این شبكه در مرجع [ 1] داده شده است. این شبكه 31 گره و 35 خط و 6 فیدر دارد. گراف شبكه بسته این شبكه توزیعدر شكل ( 3) نشان داده شده است که پنج حلقه دارد.

الگوریتم دایسترا برای شبکه فوق در 30 مرحله انجام داده ایم که در نتیجه آن در هر مرحله یک خط از شبكه بهینه تعیین گردیده است .، ترتیب خط های تعیین شده در مراحل 30 گانه عبارت است از : 1و32و20و16و11و13و18و2و4و15و33و31و35و17و34و7و24و21و3و28و14و30و25و23و26و5و29و6و8و12.بنابراین 5 خط دیگر شبكه یعنی خطوط با شماره های 9-10-19-22-27 باید باز باشند 

تلفات این آرایش 0.001506556 بدست آمده است .. 

،در شبکه فوق مجموعا 73 دفعه پخش بار پیشرو-پسرو روی فیدرها انجام گرفته است و فیدرهائی که برروی آنها پخش بار انجام شده است، بطور متوسط تعداد 5.0685 خط داشته اند. بنابراین حجم محاسبات مورد نیاز بسیار کم می باشد. کل زمان محاسبه برای بدست آوردن آرایش بهینه شبکه پنج حلقه ای فوق 0.359 ثانیه بوده است. این محاسبه توسط یک برنامه کامپیوتری با نرم افزار MATLAB در یک کامپیوتر پنتیوم 2.4 گیگاهرتز صورت گرفته است.

برای بررسی آرایش نهائی بدست آمده در بالا، تلفات تمامی آرایشهای شعاعی ممكن این شبكه توزیع را محاسبه كرده ایم و 10 آرایشی كه كمترین تلفات را دارند در جدول ( 4) بیان نموده ایم. شایان ذکر است که در این جدول خطوط باز هر آرایش بیان شده است. چنانكه در جدول مزبور ملاحظه می شود، شش آرایش اول دارای تلفات یكسان بوده و آرایش بهینه با كمترین تلفات می باشند و آرایش بدست آمده با روش پیشنهادی جزء آرایشهای بهینه (سطر ششم جدول زبر) می باشد. شایان ذکر است که در مرجع [ 4] آرایش سطر ششم و در مرجع [ 2] آرایش سطر پنجم جدول ( 4) بدست آمده است که همگی آرایش بهینه هستند.

-6 مقایسه روش پیشنهادی با برخی از روشهای قبلی

در دو مثال قبل روش پیشنهادی با روش تمام شماری(روش بررسی تمام حالات ممکن شبکه) مقایسه شد و نشان داده شد که روش پیشنهادی همواره به بهینه مطلق می رسد زیرا الگوریتم بهینه یابی دایسترا ذاتا بهینه مطلق را در اختیار می گذارد. درصورتیکه در روشهای مبتنی بر جسجوی ابتکاری و الگوریتم ژنتیک و شبیه سازی ذوب فلزات، هیچ تضمینی برای رسیدن به آرایش بهینه مطلق وجود ندارد و ممکن است به یک بهینه موضعی برسند. بطور مثال در مرجع [ 8] که مبتنی بر الگوریتم ژنتیک است بیان شده است که در تمام شبکه ها، روش الگوریتم ژنتیک به جواب بهینه مطلق نمی رسد و فقط جواب نیمه بهینه خوبی در اختیار می گذارد.

از طرفی در دو مثال قبل نشان داده شد که حجم محاسبات مورد نیاز در روش پیشنهادی نسبتا کم بوده و زمان محاسبات بسیار کوتاه است بطوریکه استفاده از این روش برای کاربردهای زمان واقعی مناسب می باشد.

این درحالیست که روشهای الگوریتتم ژنتیک و شبیه سازی ذوب فلزات با توجه به اینکه در اکثر موارد به آرایشهای غیر ممکن برخورد میکنند ونیاز به تولید آرایش دیگری دارند؛ زمانهای بسیار طولانی تری می برند.

تفاوت دیگر روش پیشنهادی نسبت به سایر روشها این است که رسیدن به آرایش بهینه با اضافه کردن مرحله ای خطوط بدست می آید می توان در هر مرحاه محدودیتها ئی مثل حداکثر افت ولتاژ مجاز یا حداکثر توان انتقالی را بررسی نموده و در صورت عدم رعایت آن، خط مربوطه را کنار گذاشت و به جای آن خط دیگری از آن مرحله که تلفات کمتری را دارد به آرایش قبلی اضافه نمود. شایان ذکر است که در اکثر روشهای جستجوی ابتکاری، آرایش بهینه با باز کردن مرحله ای یک خط از شبکه حلقوی بدست می آید.

-7 نتایج بخش

با تجدید آرایش شبكه های توزیع می توان آرایش شعاعی را بدست آورد كه تلفات آن حداقل باشد. از آنجائیكه تعداد آرایشهای یك شبكه توزیع بسیار زیاد است و امكان بررسی تمامی آرایشها نیست؛ لذا الگوریتم دایسترا (در نظریه گراف) برای یافتن آرایش بهینه پیشنهاد گردید. نحوه کاربرد الگوریتم مزبور برای دو شبکه توزیع نمونه یک حلقه ای و پنج حلقه ای در طول مقاله نشان داده شد و نتایج زیر بدست آمد:

-1 در هر مرحله از الگوریتم دایسترا، شبکه های مورد بررسی شعاعی هست ند بنابراین در هر بررسی فقط پخش بار شعاعی مورد نیاز است . لذا در این مقاله پخش بار شعاعی پیشرو -پسرو پیشنهاد شده است که مخصوص شبکه های شعاعی بوده و از سرعت بسیار بالائی برخوردار می باشد.

-2 در الگوریتم دایسترا، در هر دفعه که بایستی تلفات را محاسبه کنیم فقط ساختار یکی از فیدرها تغییر کرده است . بنابراین انجام پخش بار برای فقط یکی از فیدرهای شبکه کافی است و نیاز به انجام پخش بار برای کلیه فیدرها نمی باشد. لذا محاسبات بسیار کم می شود.

-3 در الگوریتم دایسترا، بسیار اتفاق می افتد که محاسبه تلفات یک فیدر با یک سا ختار ثابت در دو یا چند مرحله تکرار می شود . لذا می توان اطلاعات تلفات فیدرها را در هر مرحله ذخیره نمود و در نتیجه تعداد پخش بارهای مورد نیاز را بسیار کاهش داد.

-4 با توجه به بندهای سه گانه فوق حجم محاسبات مورد نیاز برای الگوریتم دایسترا بسیار کم است و چنانکه توسط شبکه های نمونه هم نشان داده شد سرعت تعیین آرایش بهینه بسیار بالا می باشد و برای استفاده کاملا مناسب است. (Real Time) در زمان واقعی

-5 چنانکه نشان داده شد؛ الگوریتم دایسترا همواره آرایش بهینه مطلق را در اختیار می گذارد و مانند روشهای ابتکاری و یا روشهایی نظیر الگوریتم ژنتیک در بهینه موضعی گیر نمی کند.